En esta ocasión, reconozco que no os lo voy a poner fácil, pero si sois capaces de entender los conceptos que veremos a continuación, podréis encontrar algunas operaciones MUY interesantes creando Calendar Spreads.
Los Calendar Spreads son estructuras complejas. La mayoría de los traders no entienden realmente la dinámica de estas estrategias, y por esa razón es muy raro encontrarse con alguien en el espacio retail que los opere correctamente.
Antes de entrar en materia, un aviso importante: personalmente creo que hay una enorme ventaja si operamos sobre la base de los conceptos tratados en este post, por cuanto no hay mucha gente que profundice en estas cosas.
Para los traders dispuestos a pasar el tiempo buscando volatilidad a plazo mal valorada, sin duda hay algunas grandes oportunidades.
Definición de Calendar Spread
Un Calendar Spread es una estructura de trading con opciones en la que compramos y vendemos la misma opción con el mismo precio de ejercicio en 2 vencimientos diferentes.
Para mayor simplicidad, en este artículo nos centraremos en los Calendar Spreads largos. Un Calendar Spread largo consiste en vender el vencimiento más cercano y comprar el vencimiento más lejano. Un ejemplo de un Calendar Spread largo sería vender AAPL Jul 150 Call y comprar Sep 150 Call.
Un Calendar Spread corto sería lo contrario: comprar el mes más cercano y vender el más lejano.
A continuación se muestra un ejemplo de un Calendar Spread largo.
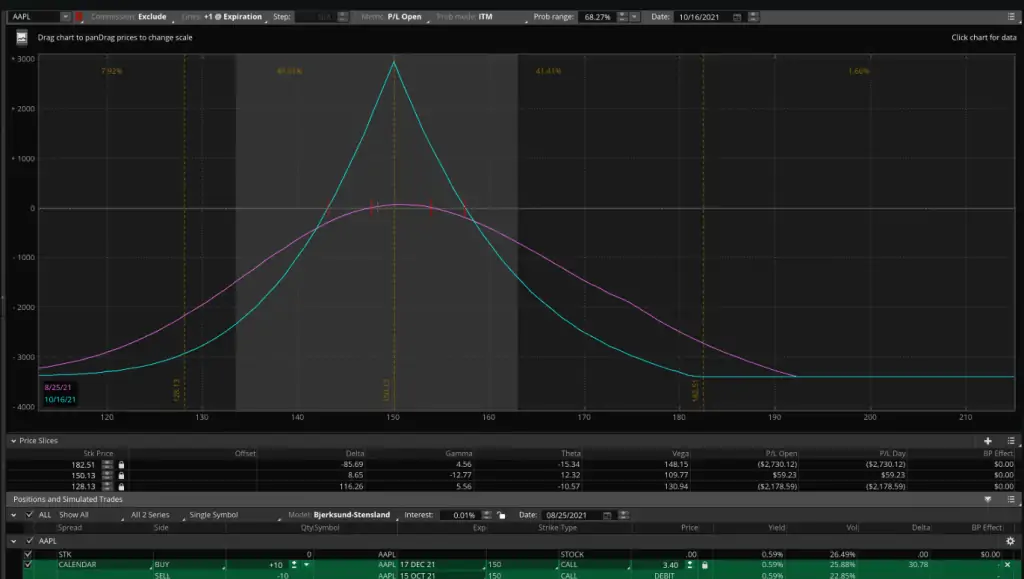
El Calendar Spread comprado del ejemplo tiene una pérdida máxima del débito pagado. En el ejemplo anterior, el máximo que podemos perder es $3.40 o $340 por calendar.
Qué dice un Calendar en el Mercado
La clave para un trading rentable es tener una visión del mundo y luego expresar esa visión lo mejor posible.
Si su opinión es correcta y la ha expresado bien, ganará dinero. Tener una opinión incorrecta o expresarla de forma incorrecta dará lugar a pérdidas.
Por esa razón, con cualquier estructura es una buena idea empezar por entender cómo se moverá nuestro PnL en diferentes escenarios.
Para hacer esto examinaremos nuestra exposición al mercado, es decir, las griegas de nuestra posición.
De un vistazo rápido, en un Calendar ATM:
- Delta neutral – al inicio de la operación, nos es indiferente la dirección de la acción.
- Gamma corta – los movimientos rápidos perjudicarán nuestra posición.
- Theta larga – en igualdad de condiciones, con el paso del tiempo ganaremos dinero.
- Vega larga – un aumento de la volatilidad implícita nos hará ganar dinero (Nota: en realidad, pensar que esta estructura es Vega larga es un error común de muchos traders. Más sobre esto un poco más adelante.
En resumen:
- En apariencia parece que el Calendar será rentable si no pasa nada o si hay una gran explosión en la volatilidad implícita.
- Asimismo el Calendar perderá dinero si se produce un movimiento brusco en el precio de la acción.
Una Apuesta Sobre la Volatilidad a Plazo. Lo que un Calendar es en Realidad
En este punto donde la mayoría de la gente se suele confundir.
Un Calendar Spread es en realidad una operación de valor relativo entre gamma y vega.
Se puede ver como «estoy corto de gamma y cubriéndome con vega».
O también puede verse como una apuesta por la «volatilidad a plazo».
Pero, ¿qué es la volatilidad a plazo? Veamos un ejemplo. Supongamos el siguiente escenario:
A 1 de junio las volatilidades implícitas son las siguientes:
- Vencimiento 1 de julio: 40%
- Vencimiento 1 de septiembre: 35%
¿Qué conclusiones podemos sacar ya que conocemos la volatilidad implícita de estos dos vencimientos? Sabemos que en los próximos 30 días, el vencimiento del 1 de julio, la volatilidad implícita es del 40%. También sabemos que en los próximos 90 días, el 1 de septiembre, la volatilidad implícita es del 35%.
Pero aquí hay una pregunta para Vd., querido lector: ¿qué está implícito entre 30 y 90 días?
En otras palabras, ¿cuál será la volatilidad de septiembre una vez que expire julio? Eso es lo que es la «volatilidad a plazo». Concretamente sería la 30/90 Forward vol.
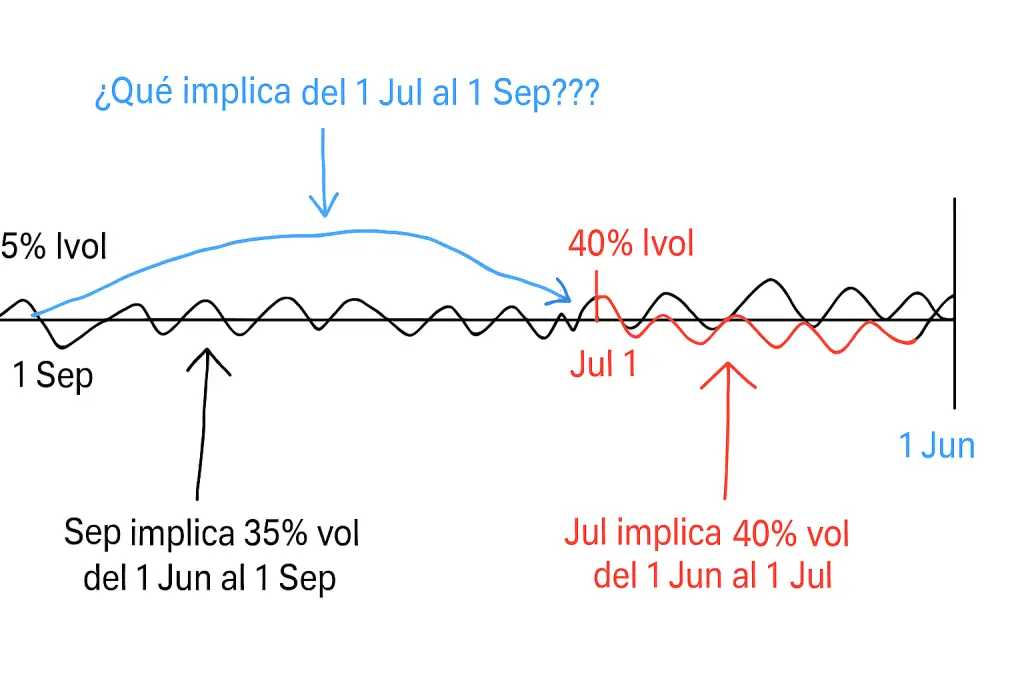
No voy a poneros complicadas fórmulas matemáticas aquí (podéis encontrarlas fácilmente haciendo algunas búsquedas). Simplemente tenéis que quedaros con que, en este ejemplo, la volatilidad a plazo 30/90 sería del 32%. Si compramos este Calendar estaríamos comprando volatilidad a plazo al 32%.
Los Calendars son en realidad un juego de valor relativo entre gamma y vega.
La siguiente parte será un poco más difícil de entender, pero es importante que lo entendáis completamente.
Cuando operamos con el Calendar Julio/Septiembre, la exposición de julio tendrá mucha más gamma que nuestra exposición de septiembre. Por otro lado, nuestro septiembre tendrá más vega.
Vendimos julio con una volatilidad implícita del 40% y compramos septiembre con una volatilidad implícita del 35%. De este modo, nos aseguramos una volatilidad a plazo del 32%.
Ahora imaginemos que en los próximos 30 días la volatilidad es del 40%.
Eso implicaría un punto de equilibrio en nuestra exposición de julio.
Ahora viene la pregunta complicada… ¿a qué precio cotizará septiembre?
Si septiembre cotiza por encima de 32 habremos ganado dinero con el Calendar y si cotiza por debajo de 32 habremos perdido dinero.
Ahora empecemos a jugar con diferentes escenarios….
Si se materializa una volatilidad de 60 en los próximos 30 días, habremos perdido con el vencimiento de julio ya que vendimos a 40. Pero ahora septiembre debería estar cotizando mucho más alto, ¿verdad?
La mayor parte del PnL de julio viene de la gamma y la mayor parte del PnL de septiembre viene de la vega.
Hagamos un ejemplo más: imaginemos que se materializa una volatilidad de 10 en los próximos 30 días.
En este caso, vamos a ganar mucho dinero en nuestra posición de julio desde que vendimos a 40.
¿Y en septiembre?
Bueno, si solo se materializa una volatilidad de 10, ¡la volatilidad implícita de septiembre caerá mucho!.
Por lo tanto, en este ejemplo ganamos dinero con la gamma y perdemos dinero con la vega.
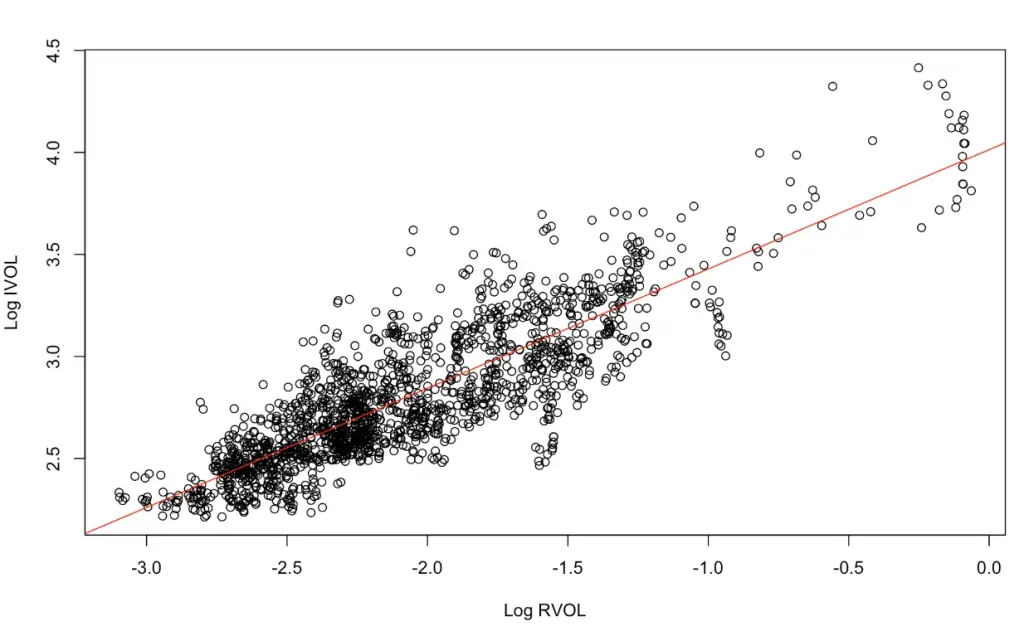
El siguiente gráfico muestra la relación entre la volatilidad implícita y la volatilidad realizada para el QQQ.
La fuerte relación indica que rara vez se pierde dinero tanto en gamma como en vega o se gana dinero en ambas patas, ya que cuando RVOL es alta, IVOL suele ser alta y viceversa.
A continuación se muestra un gráfico de series temporales de la volatilidad a plazo 30/90 de AAPL. Este gráfico es importante para montar Calendar Spreads ya que nos permite examinar donde está la volatilidad a plazo 30/90 actual en relación a su evolución histórica.
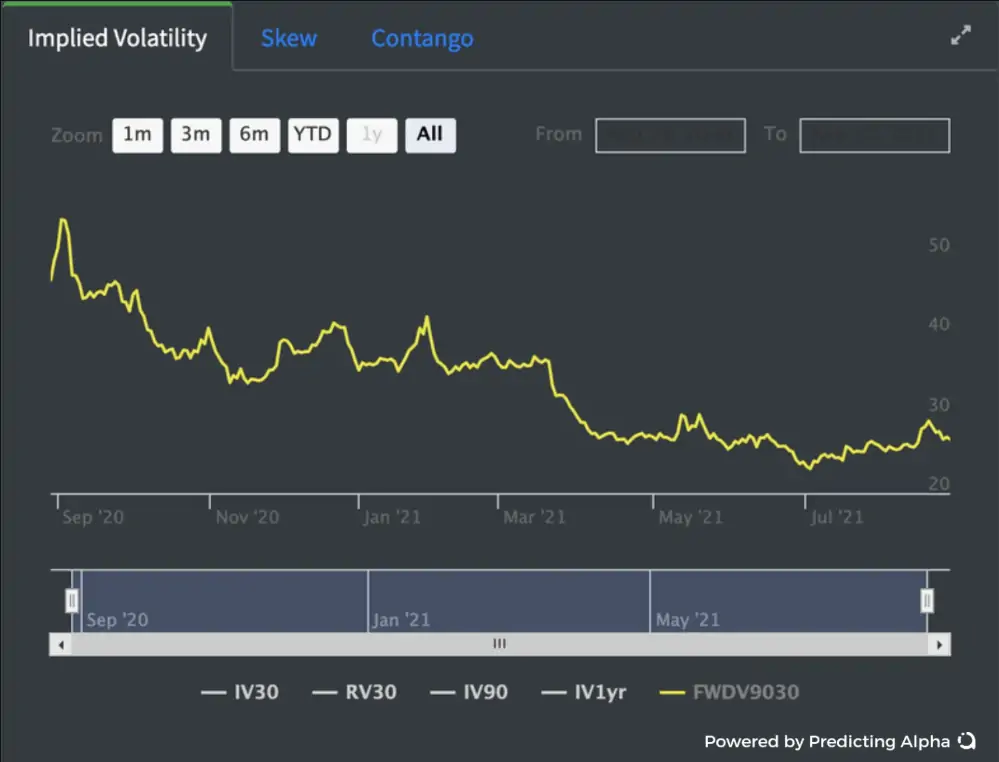
Plano en Vega, Plano en Raíz del Tiempo
Ahora que nos hemos quitado esto de encima, ¡vamos a ponerlo incluso un poco más difícil! (Y ojo porque esta es la razón por la que los Calendars no deben ser negociados por la mayoría).
Para encontrar ideas de trading necesitamos entender cómo se mueve la estructura a plazo.
La estructura a plazo es un término utilizado para describir cómo se ve la volatilidad implícita en diferentes vencimientos. En el siguiente gráfico podéis ver un ejemplo de la estructura a plazo de AAPL en 2 días diferentes (19 y 26 de agosto).
Podéis ver que las opciones a 30 días cotizan al X% y las opciones a 90 días cotizan al Y%. También podéis ver que en un periodo de 1 semana la volatilidad a través de la estructura a plazo ha caído (la volatilidad implícita ha bajado en todos los plazos respecto a una semana antes, de tal forma que la curva del 19 de agosto está por encima de la del 26 para cualquier vencimiento futuro).
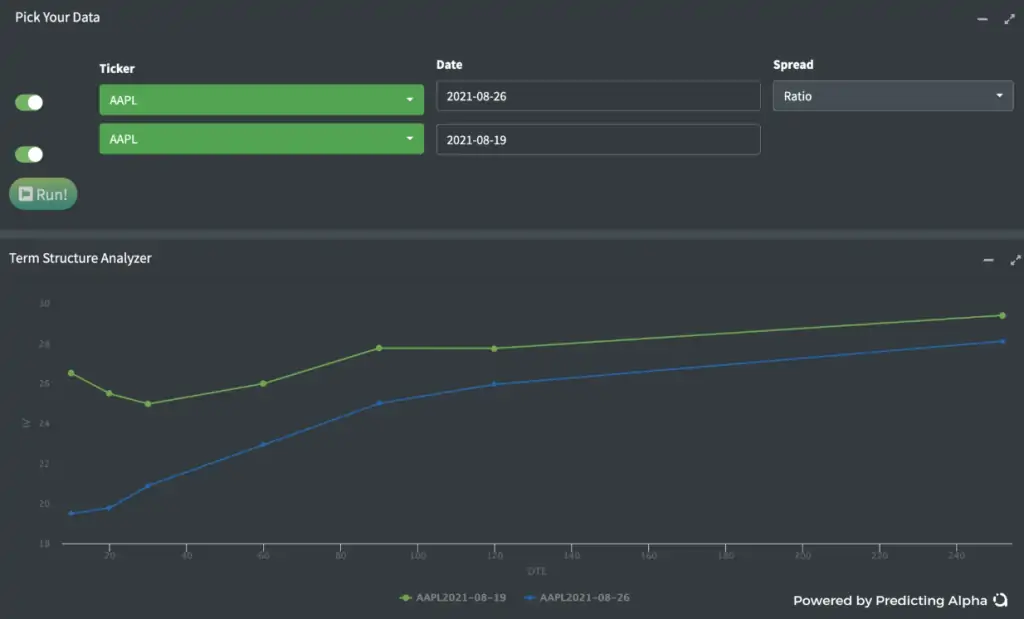
Es importante que entendamos cómo se mueve «normalmente» la estructura temporal. La estructura temporal se mueve en base a la «raíz cuadrada del tiempo».
En pocas palabras, esto significa que las opciones a corto plazo son más sensibles que las opciones a largo plazo. Sensible significa cuánto se mueven en términos de volatilidad implícita.
La mejor manera de explicar esto es mostrando un ejemplo. Supongamos que tenemos una estructura a plazo plana:
- IV a 30 días = 30%
- IV a 60 días = 30%
- IV a 90 días = 30%
- IV a 120 días = 30%
- IV a 365 días = 30%
Supongamos que mañana se produce un «shock»: China decide interrumpir el comercio internacional con Estados Unidos (algo que ahora mismo no parecería muy descabellado, dados los tiempos que corren 😅).
Esto provocaría un aumento de la volatilidad.
Si la IV a 365 días sube del 30% al 40%, lo que querremos saber es, ¿cuánto deberían cambiar los otros vencimientos?
La respuesta la tenemos en… ¡la raíz cuadrada del tiempo!
La volatilidad a 1 año ha variado 10 puntos. Esto significa que la IV a 30 días habrá cambiado en Raíz(365/30) x Var. Volatilidad anualizada + IV a 30 días. Por su parte, la IV a 60 días cambiará en Raíz(365/60) x Var. Volatilidad anualizada + IV a 60 días.
A continuación se muestra como quedan nuestros multiplicadores:
- Raíz(365/30) = 3,48
- Raíz(365/60) = 2,46
- Raíz(365/90) = 2,01
- Raíz(365/120) = 1,74
- Raíz(365/365) = 1
Así que nuestra nueva volatilidad será:
- IV a 30 días = 3,48 x 10 + 30 = 65% (aumento de 35 puntos)
- IV a 60 días = 2,46 x 10 + 30 = 55% (aumento de 25 puntos)
- IV a 90 días = 2,01 x 10 + 30 = 50% (aumento de 20 puntos)
- IV a 120 días = 1,74 x 10 + 30 = 47,5% (aumento de 17,5 puntos)
- IV a 365 días = 1 x 10 + 30 = 40% (aumento de 10 puntos)
En el siguiente gráfico podemos ver cómo cambiar la estructura a plazo tras el shock:
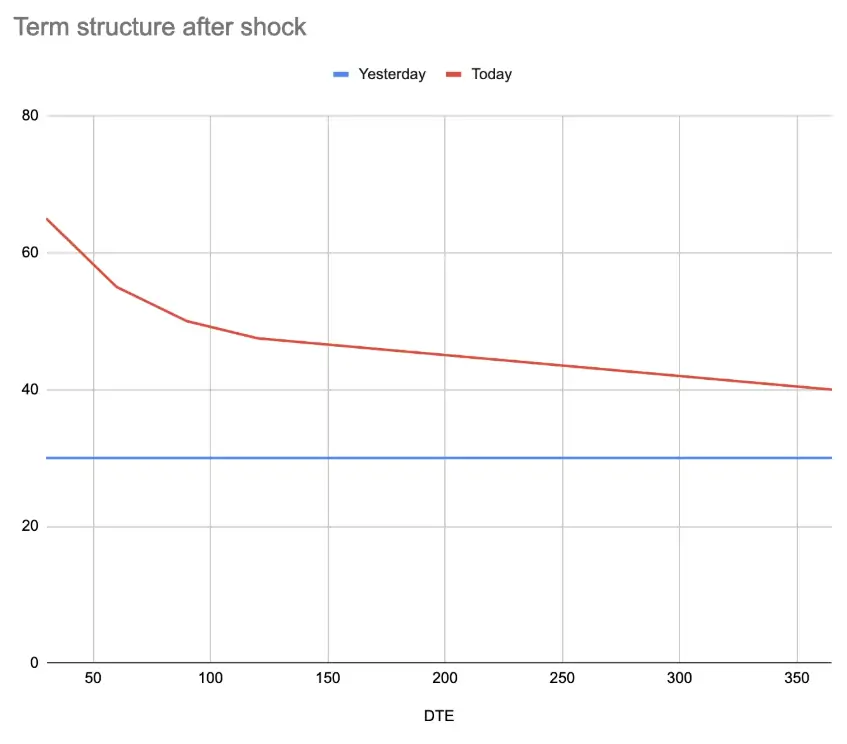
Algunos traders intentan operar contra cualquier movimiento que no sea el resultado de aplicar la raíz del tiempo, por lo que si la IV a 90 días sólo se moviera al 45%, entonces comprarían ese vencimiento y venderían los vencimientos circundantes utilizando un Calendar Spread.
Y para remate, un hecho que es realmente interesante también: la vega también se mueve con la raíz del tiempo a través de la cadena de opciones. Por ejemplo, si miramos las opciones ATM de Apple tenemos que:
- Vega 30 días = 17
- Vega 60 días = 24
- Vega 90 días = 29
- Vega 120 días = 34
- Vega 365 días = 59
Recordemos que la vega es nuestra sensibilidad al cambio en la volatilidad implícita. Por ejemplo, si mi vega para una opción es 10 y la volatilidad implícita aumenta 1 punto de 30 a 31, entonces ganaré 1 x 10 (exposición vega) o 10 $.
Veamos como queda nuestro PnL para nuestro escenario anterior cuando la volatilidad a 1 año aumentó un 10% (de 30 a 40). Sabiendo que Call $PnL = Incremento en puntos x vega, tenemos que:
- PnL Call a 30 días = 35 x 17 = $595
- PnL Call a 60 días = 25 x 24 = $600
- PnL Call a 90 días = 20 x 29 = $580
- PnL Call a 120 días = 17,5 x 34 = $595
- PnL Call a 365 días = 10 x 59 = $590
A pesar de que nuestro Calendar parecía inicialmente largo en vega, ¡resulta que un shock de la volatilidad nos puede dejar con las manos vacías!
Todas las Calls ganaron la misma cantidad de dinero (aunque con ligeras variaciones por redondeo).
Esto nos dice que nuestro Calendar en realidad no es long vega sino algo llamado «root time flat» (plano en raíz del tiempo). Esto significa que si se producen movimientos normales a lo largo de la estructura temporal, no perderemos ni ganaremos dinero debido a nuestra exposición a la vega.
Un Poco de Alfa de Regalo
Seguramente ahora el lector se esté preguntando, ¿y cómo puedo ganar dinero con la vega usando un Calendar Spread «root time flat»?
La respuesta es que ganaremos/perderemos dinero gracias a movimientos no basados en la raíz cuadrada del tiempo.
Veamos un ejemplo en el que ganaríamos dinero. Digamos que nos enteramos de que una compañía farmacéutica va a lanzar un nuevo medicamento el 1 de septiembre. Miramos la cadena de opciones sobre las acciones de esta compañía y vemos que la volatilidad implícita a plazo es la siguiente:
- Julio – 30%
- Agosto – 30%
- Septiembre: 30%
- Octubre: 30%.
Bien, sabemos que debería haber una gran noticia en septiembre, ¿verdad? Así que los contratos de septiembre deberían cotizar más alto que los de julio y agosto. ¡Pero esto no es así!
Por tanto, lo que podemos hacer es vender agosto y comprar septiembre.
De esta manera, cuando septiembre finalmente recoja el impacto de la publicación del fármaco, la volatilidad de septiembre aumentará y ganaremos dinero con nuestro Calendar Spread.
¿Por qué? Porque se habrá producido un movimiento no basado en la raíz del tiempo – agosto no ha cambiado pero la volatilidad de septiembre podría aumentar del 30% al 40%. Como estamos largos en volatilidad de septiembre, ganaremos dinero.
Conos de Volatilidad
Una buena herramienta para encontrar situaciones caras y baratas en la estructura a plazo es el «cono de volatilidad».
Con un cono de volatilidad podemos ver dónde han estado las volatilidades implícitas para diferentes plazos, lo que nos dará una idea relativa de si ahora están caras o baratas.
Por ejemplo, mirando la siguiente imagen, supongamos que viéramos una estructura a plazo en la que IV30 fuera 80 e IV120 también.
Supondríamos que con una estructura temporal tan plana a esos niveles, las volatilidades a largo plazo están sobrevaloradas en relación con las volatilidades a corto plazo. Especialmente si la acción está realizando una volatilidad de 100. Para realizar esta operación podríamos hacer un Calendar Spread inverso, vendiendo el vencimiento más lejano y comprando el más cercano. De este modo, expresaríamos la opinión de que la gamma está barata en relación con la vega.
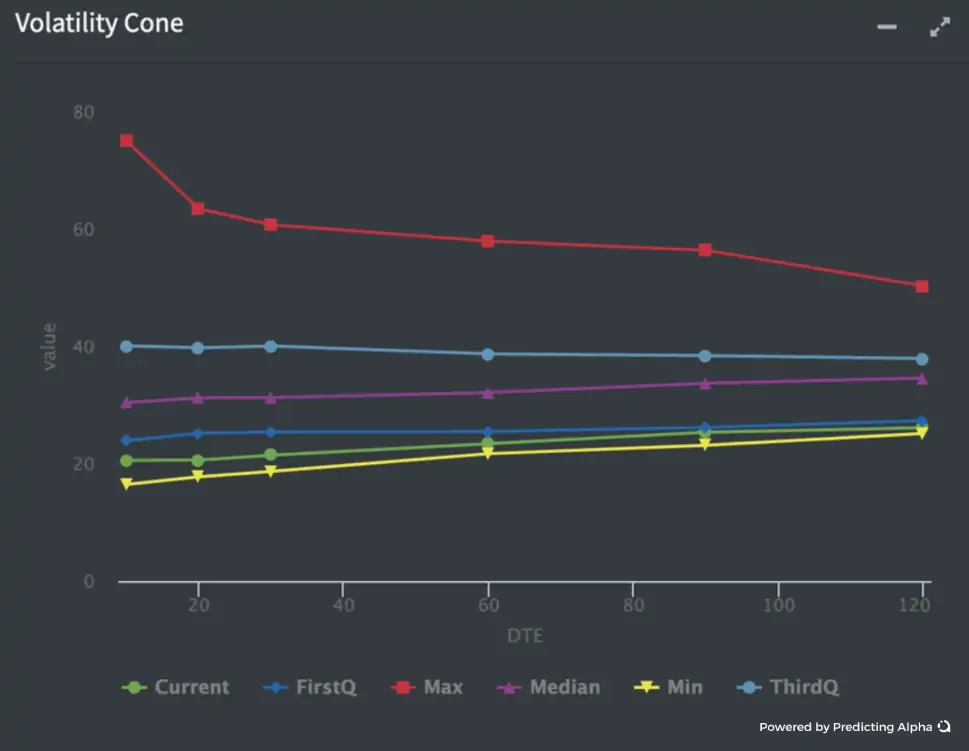
Conclusión
Posiblemente esta entrega haya sido la parte más complicada de todo lo que llevamos hasta el momento. Sin embargo, analizar esta complejidad merece la pena, por cuanto hay algunas oportunidades de trading realmente interesantes una vez que se comprende a fondo la dinámica de estos Calendars.
Recuerde siempre que a partir de nuestra creatividad y de la generación de ideas es de donde vendrá el alfa. Y es evidente que aprender sobre estos Calendars y empezar a analizarlos le va a ayudar a generar multitud de ideas operativas.
(Continuará…)
Saludos,
X-Trader