¿Qué tienen que ver los granos de polen, las distribuciones de probabilidad y los fractales con los mercados financieros? En esta entrega de la serie introducimos el concepto de fractal y su relación con las dimensiones espaciales.
El Jugador Francés y los Granos de Polen
En 1827 el botánico inglés Robert Brown puso sus manos sobre una nueva tecnología: un microscopio hecho a medida. De inmediato, Brown observó cómo los granos de polen en suspensión en el agua se agitaban de forma vibrante pero aleatoria. Exactamente algo como esto:
Lo que estaba pasando era un enigma. Mucha gente se preguntaba: estos pequeños trozos de materia orgánica de alguna manera ¿tenían vida? Por suerte, Hollywood no vivía en aquella época, si no John Carpenter podría haber hecho su maravillosa película de terror ¡Están vivos!.
El propio Robert Brown pensaba que el movimiento no tenía nada que ver con pequeñas corrientes en el agua, ni se producían por la evaporación.
Brown sabía que otros antes de él habían hecho observaciones similares en casos especiales. Por ejemplo, el Dr. James Drummond había observado este movimiento errático en los ojos del pescado:
Actualmente sabemos que este movimiento, llamado movimiento browniano en honor a Robert Brown, se debe a las fluctuaciones aleatorias en el número de moléculas de agua que bombardean los granos de polen desde diferentes direcciones.
Los experimentos mostraron que las partículas se movían más en un intervalo de tiempo dado si la temperatura aumentaba, se reducía el tamaño de la partícula o se reducía la «viscosidad» del fluido. En 1905, en un célebre tratado titulado The Theory of the Brownian Movement, Albert Einstein desarrolló una descripción matemática que explicaba el movimiento browniano en estos términos. Más tarde, en 1923, Norbert Wiener dio una descripción matemáticamente rigurosa de lo que ahora se conoce como un «proceso estocástico». Desde ese momento, el movimiento browniano paso a denominarse proceso de Wiener y también proceso de difusión o paseo aleatorio.
Pero Einstein no fue el primero en hacer una descripción matemática del movimiento browniano. Ese honor le pertenecía a un estudiante graduado francés al que le gustaba apostar. Su nombre era Louis Bachelier. Al igual que muchas personas, que buscaba combinar el deber con el placer, en 1900 en París presentó su tesis doctoral, titulada Théorie de la Spéculation.
Lo que interesaba a Bachelier no eran los granos de polen o los ojos de pez. En su lugar, lo que quería saber era por qué los precios de las acciones y los bonos se “agitaban” en la Bolsa de París. Estaba particularmente intrigado por los bonos conocidos como rentes sur l’état (bonos perpetuos emitidos por el gobierno francés). ¿Cuáles eran las leyes que regían la “agitación”? se preguntaba Bachelier. Su hipótesis era que los precios son bombardeados por pequeños bits de noticias.
La Raíz Cuadrada del Tiempo
Entre otras cosas, Bachelier observó que los intervalos de probabilidad en la que caen los precios parecían aumentar o disminuir con la raíz cuadrada del tiempo (T0.5). Esta fue una idea clave.
Por «intervalo de probabilidad» nos referimos a una determinada probabilidad para un rango de precios. Por ejemplo, los precios podrían caer dentro de determinado rango de precios con el 65% de probabilidad durante un año. Pero si tomamos más de dos años, el mismo rango de precios que se dará con un 65% de probabilidad será mayor que durante un año. ¿Cuánto más grande? Bachelier dijo que el cambio en el nivel de precios era proporcional a la raíz cuadrada del tiempo.
Sea P el precio actual. Después de un tiempo T, los precios (con una probabilidad dada) estarán en el rango:
(P-aT0.5, P+aT0.5)
siendo a una constante.
Por ejemplo, si T representa un año (T = 1), entonces la última ecuación se simplifica a
(P-a, P+a).
La variación de los precios de más de dos años (T = 2) sería:
aT0.5 = a(2)0.5 = 1.4142a
Es decir, 1.4142 veces la variación a lo largo de un año. Por el contrario, la variación para medio año (T = 0.5) sería:
aT0.5 = a(0.5) 0.5 = 0.7071 a
Esto es, aproximadamente el 71% de la variación en un año completo. Es decir, después de 0.5 años, el precio (con una probabilidad dada) estaría en el rango
(P-0.7071a, P+0.7071a)
Aquí la constante a tiene que ser determinada, pero se supone que será diferente para diferentes tipos de precios: a puede ser más grande para los precios de la plata que para los precios del oro, por ejemplo. Puede ser más grande para las acciones de Yahoo! que para las acciones de IBM.
Por tanto, el rango de precios para una probabilidad dada depende de la constante a, y de la raíz cuadrada del tiempo (T0.5). Esta fue la intuición de Bachelier.
Normal frente a Lognormal
No obstante, Bachelier cometió un error financiero. Recordemos que en finanzas siempre tomamos logaritmos de los precios. Esto es por muchas razones. La mayoría de los cambios en la mayoría de las variables económicas son proporcionales a su nivel actual. Por ejemplo, es plausible pensar que la variación en los precios del oro es proporcional al nivel de los precios del oro: el Oro a 800 dólares varía en incrementos mayores que el oro a 260 dólares.
Las variaciones del precio, DP, como proporción del precio actual P, se pueden escribir como:
DP / P.
Pero esto es aproximadamente lo mismo que la variación en el logaritmo neperiano (Ln) del precio:
DP / P » D (Ln P).
Lo que esto significa es que Bachelier debería haber escrito su ecuación de la siguiente manera:
Ln P –aT0.5, Ln P + aT0.5
Sin embargo, tengamos en cuenta que Bachelier estaba haciendo innovaciones tanto en finanzas como en la teoría matemática del movimiento browniano, por lo que ya le costó de por sí llegar a la idea básica, sin preocuparse de dar todos los detalles para leer su tesis a una audiencia casi inexistente. Y, por cierto, casi nadie leyó la tesis doctoral de Bachelier, excepto el célebre matemático Henri Poincaré, uno de sus instructores.
El rango de precios para una probabilidad dada, por tanto, depende de la constante a, de la raíz cuadrada del tiempo (T0.5), así como del nivel de precios actual P.
Para ver por qué esto es así, tengamos en cuenta que el rango de probabilidad para el logaritmo del precio:
(Ln P – aT0.5, Ln P + aT0.5)
Se traduce en un rango de probabilidad para el precio tal que:
(P Exp(-aT0.5), P Exp(aT0.5)).
Donde Exp representa la potencia del número e=2.718281.
En lugar de sumar o restar una cantidad al precio actual P, multiplicamos algo por el precio actual P. Así que la respuesta depende del nivel de P. Por ejemplo, para un período de medio año (T = 0.5), en lugar de:
(P-0.7071a, P+0.7071a)
Obtenemos:
(P Exp (-0.7071a), P Exp (0.7071a))
El primer intervalo tiene un ancho constante de 1.4142a, sin importar el nivel de P (P + 0,7071 porque P + 0.7071a – (P -00.7071a) = 1.4142a). Sin embargo, la anchura del segunda intervalo varía con P. Si duplicamos el precio P, la amplitud del intervalo se dobla también.
Bachelier permitió que el rango de precios dependiera de la constante a y de la raíz cuadrada del tiempo (T0.5), pero omitió el requisito de que el rango de precios también debe depender del nivel de precios actual P.
La diferencia entre los dos enfoques es que si los incrementos de precios (DP) son independientes, y tienen una varianza finita, entonces el precio P tiene una distribución Normal o gaussiana. Pero si los incrementos en el logaritmo del precio (D Ln P) son independientes, y tienen una varianza finita, entonces el precio P tiene una distribución Lognormal.
En el siguiente gráfico tenemos una distribución Normal o gaussiana:
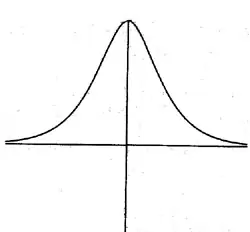
La cola de la izquierda nunca llega a ser cero. No importa donde centremos la distribución, siempre hay una pequeña probabilidad positiva para los números negativos.
En el caso de una distribución Lognormal:
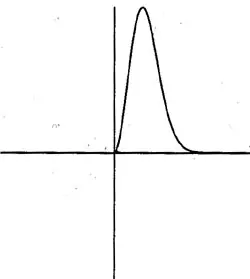
Una distribución lognormal asigna una probabilidad cero a los precios negativos, algo bastante lógico teniendo en cuenta que no es habitual que los precios lo sean.
¿Cómo Es de Grande?
Cambiemos un poco de tema: vamos a pasar ahora de las distribuciones de precios a la cuestión de cómo medir las cosas, lo que nos llevará de Bachelier a Mandelbrot.
Por lo general, cuando medimos las cosas, usamos las dimensiones habituales. Un punto tiene dimensión cero. Una línea tiene una dimensión. Un cuadrado tiene dos dimensiones. Un cubo tiene tres dimensiones. Estas dimensiones básicas, de sentido común, son lo que se conoce como dimensiones topológicas.
Supongamos que tenemos una sala de 10×10 metros, o 100 metros cuadrados. ¿Qué tamaño debe tener la moqueta que necesitamos para cubrir toda la sala? Evidentemente 100 metros cuadrados.
Sin embargo, dividamos cada lado de la sala por 10:

Se obtienen 100 piezas. Es decir, si se divide por un factor de escala 10, se obtienen 100 cuadrados más pequeños, cada uno de los cuales se parecen a la sala original. Si multiplicamos cualquiera de los cuadrados más pequeños por 10, obtendremos el gran cuadrado original.
Vamos a calcular una dimensión para este cuadrado. Utilizando la misma fórmula que se utilizó para la alfombra de Sierpinski (ver artículo anterior) tenemos que:
N = rD
Tomando logaritmos, tenemos que Ln N = D Ln r, o D = Ln N / Ln r.
Tenemos N = 100 piezas, y r = 10, por lo que tenemos que la dimensión D es:
D = Ln (100) / Ln (10) = 2.
Llamaremos a la dimensión D calculada de esta manera (es decir, comparando el número de objetos similares N que tenemos a diferentes escalas para el factor de escala r) una dimensión de Hausdorff. En este caso, la dimensión de Hausdorff coincide con la dimensión ordinaria o topológica, es decir, 2.
Así que, en cualquier caso, la dimensión es 2, tal y como sospechábamos desde el principio. Pero supongamos que queremos cubrir la superficie de la sala con la alfombra de Sierpinski. ¿Cuánto alfombra necesitaremos entonces?
Hemos visto en la primera parte de esta serie que la alfombra de Sierpinski tenía una dimensión de Hausdorff D = 1.8927 … Una alfombra de Sierpinski, que tenga 10 metros a cada lado tendría solo N = 101.8927 = 78.12 metros cuadrados de material en ella.
¿Por qué una alfombra de Sierpinski con 10 metros a cada lado no puede ocupar 100 metros cuadrados de material? Evidentemente porque la alfombra de Sierpinski tiene agujeros.
Recordemos que cuando dividimos el lado de una alfombra de Sierpinski por 3, solo obtenemos 8 copias del original, porque eliminamos el cuadrado del centro. Por ello, tiene una dimensión de Hausdorff de D = Ln 8 / Ln 3 = 1.8927. A continuación, dividimos cada una de las 8 copias por 3 otra vez, retiramos los cuadrados centrales una vez más, dejando 64 copias del original. Dividiendo por 3 dos veces, que es lo mismo que dividir por 9, volvemos a calcular nuestra dimensión, que nuevamente es D = Ln 64 / Ln 9 = 1.8927.
Una alfombra ordinaria tiene una dimensión de Hausdorff de 2 y una dimensión topológica (ordinaria) de 2. Una alfombra de Sierpinski tiene una dimensión de Hausdorff de 1.8927 y una dimensión topológica de 2.
A partir de este resultado, Benoit Mandelbrot define un fractal como un objeto cuya dimensión de Hausdorff es diferente de su dimensión topológica. Así que una alfombra de Sierpinski es un fractal. Una alfombra ordinaria evidentemente no es un fractal.
Los fractales son baratos y atractivos. Una alfombra de Sierpinski necesita sólo 78.12 metros cuadrados de material para cubrir 100 metros cuadrados de espacio. Al necesitar menos material, una alfombra de Sierpinski cuesta menos. Claro que tiene agujeros en ella. Pero los agujeros forman un patrón muy bien cuidado. Así que una alfombra de Sierpinski es atractiva. Barata y atractiva. No se puede superar eso.
La Historia del Primer Fractal
Pasamos a conocer el primer fractal conocido, creada en 1870 por el provocador matemático Georg Cantor.
Recordemos que nosotros creamos un fractal formando patrones similares a diferentes escalas, como lo hicimos con la alfombra de Sierpinski. Es una tarea llena de agujeros. Con el fin de obtener una alfombra cuya dimensión de Hausdorff fuera menor de 2, creamos un patrón de agujeros en la alfombra. Así que terminamos con un objeto cuya dimensión de Hausdorff D era mayor de 1 pero menor de 2, lo que hacía que la alfombra de Sierpinski sea un fractal, al ser su dimensión de Hausdorff diferente de su dimensión topológica.
Lo que George Cantor creó fue un objeto cuya dimensión era más que 0 pero menor que 1. Es decir, un objeto lleno de agujeros que era más que un punto (con 0 dimensiones) pero menos de una línea (con 1 dimensión). Es lo que se conoce como polvo de Cantor.
Para crear el polvo de Cantor, trazamos una línea, la dividimos en 3 y quitamos el tercio de en medio:
0________________________________________________________1
0__________________ 1/3 2/3 _____________________1
Ahora cortamos los medios tercios medio de cada una de las dos rectas que hemos obtenido:
0____ 1/9 2/9 ____1/3 2/3 ____ 7/9 8/9 ____1
Realizando este proceso de forma repetida obtenemos un gráfico como el siguiente:
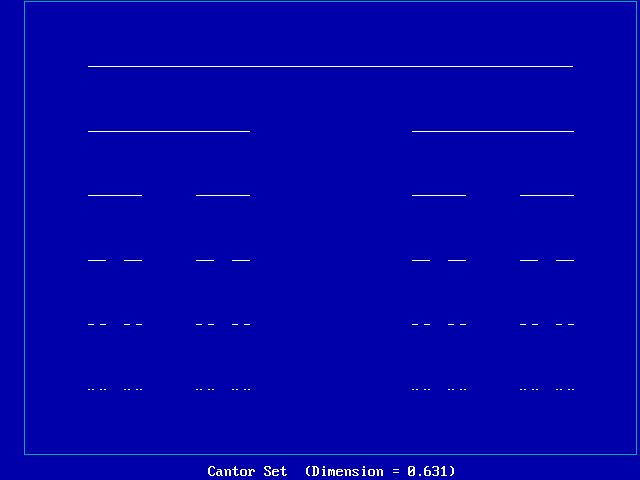
El resultado es lo que se conoce como polvo de Cantor.
En cada paso cambiamos la escala en r = 3, ya que hemos dividido cada parte restante en 3 piezas. (Cada una de estas piezas tenía un tercio de la longitud de la pieza original) Entonces nos deshicimos de la pieza intermedia. Eso nos deja 2 piezas. En la siguiente etapa había 4 piezas, a continuación, 8, y así sucesivamente. En cada paso el número de piezas aumenta por un factor de N = 2. Así, la dimensión de Hausdorff para el polvo de Cantor es:
D = Ln 2 / Ln 3 = 0.6309
¿Es el polvo de Cantor un fractal? Sí, ya que su dimensión topológica, que es 0, es diferente de su dimensión de Hausdorff que es 0.6309.
Tiempo Fractal
Hasta ahora hemos visto que medir las cosas es un asunto complicado. No todas las longitudes se pueden medir con una cinta métrica, ni los metros cuadrados de material de todas las alfombras se miden elevando al cuadrado el lado de la alfombra.
Muchas cosas en la vida son fractales, y siguen leyes potenciales al igual que el D de la dimensión de Hausdorff. En los mercados financieros, el tiempo también es fractal. El tiempo no siempre se mueve con los ritmos de un péndulo. A veces, el tiempo es menos que eso. De hecho, ya hemos encontrado tiempo fractal con el proceso de Bachelier, donde el logaritmo de la probabilidad sigue la ley potencial aT0.5.
Bachelier observó que si el intervalo de tiempo se multiplica por 4, el intervalo de probabilidad sólo se multiplica por 2. En otras palabras, con una escala r = 4, el número N de unidades con probabilidad similar es de N = 2. Así que la dimensión de Hausdorff del tiempo es:
D = Ln N / Ln r = Ln 2 / Ln 4 = 0.5.
Al pasar de Bachelier de Mandelbrot, la innovación no está en la observación de que el tiempo es fractal: esa fue la contribución de Bachelier. Ahora la pregunta es: ¿cuál es la dimensión fractal correcta para el tiempo en los mercados financieros? ¿Es la dimensión de Hausdorff D = 0.5, o toma otros valores? Y si la dimensión de Hausdorff de tiempo toma otros valores, ¿a dónde nos lleva esto?
La forma en que Mandlebrot formuló el problema proporciona un punto de partida:
«A pesar de la importancia fundamental del proceso de Bachelier, lo que ha dado en llamarse movimiento browniano, ahora es evidente que no tiene en cuenta los abundantes datos acumulados desde 1900 por los economistas empíricos, simplemente porque las distribuciones empíricas de los cambios de precios son por lo general demasiado «apuntadas» como para ser muestras procedentes de una distribución de Gauss.» (Mandelbrot, 1963).
¿Qué quiere decir Mandelbrot con «apuntadas»? Es hora de abrir un debate sobre probabilidad.
La Probabilidad es un Tarro de Mermelada
En efecto, la probabilidad es un tarro de mermelada que podemos untar sobre la recta de los números reales. Los lugares donde quede más mermelada serán los que presenten mayores probabilidades, mientras que los lugares donde haya menos mancha, tendrán menos probabilidad. Algunas pueden quedarse sin mermelada, por lo que su probabilidad es cero.
La clave es que sólo tenemos 100 gramos de mermelada. Así que si se unta más en un lugar, tendremos necesariamente que untar menos en otro lugar.
En el caso de la distribución normal estándar, el reparto de la mermelada tiene un espesor uniforme, acumulándose la mayor parte de la mermelada en torno a la media (situada en cero), por lo que los valores cercanos a cero serán los más probables. Por el contrario en los niveles extremos de la distribución, apenas hay mermelada.
Volviendo con Mandelbrot, ¿qué significa que la distribución de los cambios en los precios sea demasiado “apuntada” como para proceder de una distribución normal? Recordemos que si ponemos más mermelada en el centro de la distribución para hacerla más alta, tendremos que quitarla de otro sitio, ya que la cantidad que tenemos es limitada.
Vayan meditando sobre este aspecto, la respuesta la dejamos para el próximo artículo ;).
Saludos,
X-Trader